線性泛函與對偶空間
本文的閱讀等級:中級
考慮包含  個變數的
個變數的 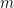 個線性聯立方程:
個線性聯立方程:
將列指標去除,針對單一方程式
等號左邊算式有兩種解釋方式。我們可以單純地將  看成是向量點積 (dot product,或稱內積),也就是
看成是向量點積 (dot product,或稱內積),也就是 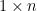 階矩陣和
階矩陣和  階矩陣乘法:
階矩陣乘法:
很容易確認  是一個從
是一個從 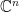 映至
映至 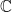 的線性變換,記為
的線性變換,記為  。為了與一般線性變換有所區隔,數學家稱這種特殊的線性變換為線性泛函 (linear functional),簡而言之,線性泛函即是將向量映射至純量的線性函數。
。為了與一般線性變換有所區隔,數學家稱這種特殊的線性變換為線性泛函 (linear functional),簡而言之,線性泛函即是將向量映射至純量的線性函數。
線性泛函的概念可以推廣至廣義向量空間。令
則  是一個線性泛函。上例中,令
是一個線性泛函。上例中,令  ,即有
,即有
值得注意的是,定義於 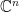 的任一線性泛函
的任一線性泛函  都具有如上式的形式,相異之處僅在於係數
都具有如上式的形式,相異之處僅在於係數  。這個性質來自線性泛函的定義。令
。這個性質來自線性泛函的定義。令  代表
代表 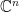 的第
的第 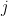 個標準單位向量,且
個標準單位向量,且
將  代入
代入  ,利用線性關係,可得
,利用線性關係,可得
定義於非幾何向量空間的線性泛函具有不同的面貌,下面給出一些例子。
例一:令
故  是一定義於
是一定義於  階矩陣的線性泛函。
階矩陣的線性泛函。
例二:這可能是數學領域中最重要的一個線性泛函。令
為一定義於 ![C([a,b]) C([a,b])](https://s0.wp.com/latex.php?latex=C%28%5Ba%2Cb%5D%29&bg=ffffff&fg=000000&s=0) 的線性泛函,原因在於積分是一線性算子。設
的線性泛函,原因在於積分是一線性算子。設  代表次數不大於
代表次數不大於 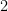 的實係數多項式構成的向量空間,其中的元素為
的實係數多項式構成的向量空間,其中的元素為  ,
, ,線性泛函可能不是一眼即可以辨識,例如,
,線性泛函可能不是一眼即可以辨識,例如,
例三:令
不難檢查確認「多項式  於
於 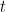 的值」是多項式空間
的值」是多項式空間  的一個線性泛函。
的一個線性泛函。
稱作 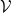 的對偶空間 (dual space),或簡記為
的對偶空間 (dual space),或簡記為  ,並滿足
,並滿足  。令
。令  是
是 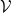 的一組有序基底。通過基底
的一組有序基底。通過基底 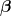 ,向量空間
,向量空間 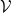 同構於 (isomorphic) 幾何座標空間
同構於 (isomorphic) 幾何座標空間 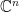 ,記為
,記為  (見“同構的向量空間”)。線性泛函是一個線性變換,
(見“同構的向量空間”)。線性泛函是一個線性變換, 有唯一的
有唯一的 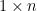 階表示矩陣
階表示矩陣  ,故
,故  可表示為 (見“線性變換表示矩陣”)
可表示為 (見“線性變換表示矩陣”)
上式中 ![[\mathbf{x}]_{\boldsymbol{\beta}} [\mathbf{x}]_{\boldsymbol{\beta}}](https://s0.wp.com/latex.php?latex=%5B%5Cmathbf%7Bx%7D%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D&bg=ffffff&fg=000000&s=0) 代表
代表 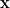 參考
參考 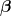 的座標向量。我們推論出線性泛函空間
的座標向量。我們推論出線性泛函空間  同構於
同構於 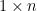 階矩陣
階矩陣  所形成的空間
所形成的空間 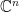 ,即
,即  。同構具有傳遞性,因此
。同構具有傳遞性,因此  。
。
既然向量空間
亦即
定義線性泛函  ,
, 。明顯地,
。明顯地, ,其中
,其中  若
若 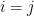 ,
, 若
若  。我們可以把
。我們可以把 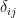 看作單位矩陣
看作單位矩陣 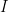 的
的  元。考慮線性泛函
元。考慮線性泛函 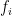 的線性組合
的線性組合
對於 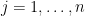 ,
,
若  ,這裡
,這裡 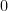 表示零函數,則
表示零函數,則  ,即有
,即有  ,
,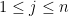 ,表明
,表明 是線性獨立集。然而
是線性獨立集。然而  ,推知
,推知  是線性泛函空間
是線性泛函空間  的一組基底,我們稱之為對偶基底 (dual basis)。由推導過程並知
的一組基底,我們稱之為對偶基底 (dual basis)。由推導過程並知 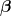 的對偶基底
的對偶基底  是唯一的。綜合以上討論,任何線性泛函
是唯一的。綜合以上討論,任何線性泛函  皆可表示成
皆可表示成
類似地,任何向量  也可表示為
也可表示為
上式提供了一個描述對偶基底的方式:若  是向量空間
是向量空間 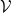 的一組有序基底且
的一組有序基底且  是對偶基底,則
是對偶基底,則 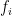 是參考
是參考 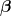 的第
的第 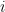 個座標函數。直白地說,
個座標函數。直白地說,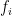 吃進向量
吃進向量  ,吐出座標向量
,吐出座標向量 ![[\mathbf{x}]_{\boldsymbol{\beta}} [\mathbf{x}]_{\boldsymbol{\beta}}](https://s0.wp.com/latex.php?latex=%5B%5Cmathbf%7Bx%7D%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D&bg=ffffff&fg=000000&s=0) 的第
的第 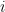 個座標值。合併上面二式可以推得這個結果:若
個座標值。合併上面二式可以推得這個結果:若  ,並令
,並令  ,
, ,則當
,則當  ,可得
,可得
這與先前得到的結果 ![f(\mathbf{x})=A[\mathbf{x}]_{\boldsymbol{\beta}} f(\mathbf{x})=A[\mathbf{x}]_{\boldsymbol{\beta}}](https://s0.wp.com/latex.php?latex=f%28%5Cmathbf%7Bx%7D%29%3DA%5B%5Cmathbf%7Bx%7D%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D&bg=ffffff&fg=000000&s=0) 完全相同。解讀如下:如果我們選擇了
完全相同。解讀如下:如果我們選擇了 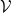 的一組有序基底
的一組有序基底 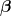 ,並稱
,並稱  參考
參考 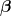 的座標向量為
的座標向量為  ,則定義於
,則定義於 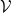 的每一個線性泛函
的每一個線性泛函  都具有上述表達式。
都具有上述表達式。
下例說明如何從
令  是
是 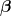 的對偶基底。利用性質
的對偶基底。利用性質  ,當
,當 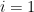 ,可得
,可得
或寫成矩陣形式:
解得  ,
, ,
, ,就有
,就有
運用類似方式,將矩陣方程等號右邊常數向量替換為  和
和  即得
即得
細心的讀者應該觀察出以  構成的三階矩陣的逆矩陣的列向量即為
構成的三階矩陣的逆矩陣的列向量即為  的係數:
的係數:
這裡面沒有甚麼玄妙之處,理由如下:
回到本文開頭給出的線性聯立方程組,以線性泛函表示為
究竟線性泛函和我們熟知的附屬於係數矩陣 ![A=[a_{ij}] A=[a_{ij}]](https://s0.wp.com/latex.php?latex=A%3D%5Ba_%7Bij%7D%5D&bg=ffffff&fg=000000&s=0) 的子空間有何關係?若
的子空間有何關係?若  是
是 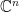 的標準基底,則其對偶基底
的標準基底,則其對偶基底  滿足
滿足  ,即
,即  ,
, 。方程式係數
。方程式係數  給出了線性泛函
給出了線性泛函 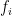 參考標準對偶基底
參考標準對偶基底  的座標向量,即
的座標向量,即
所以, 階矩陣
階矩陣  的列空間
的列空間  可視為線性泛函
可視為線性泛函  的擴張,對
的擴張,對  執行基本列運算也就是
執行基本列運算也就是  的線性組合的一種實現。再考慮求解齊次方程問題,亦即尋找
的線性組合的一種實現。再考慮求解齊次方程問題,亦即尋找  使得
使得  ,
, ,可以這麼說,尋找
,可以這麼說,尋找  的零空間
的零空間  等同於尋找可被線性泛函
等同於尋找可被線性泛函  消滅的子空間 (屬於
消滅的子空間 (屬於 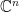 )。若以對偶觀點來看齊次方程問題,給定
)。若以對偶觀點來看齊次方程問題,給定 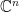 的
的 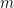 個向量
個向量  ,
, ,我們想要找出消滅這些向量的線性泛函,也就是求
,我們想要找出消滅這些向量的線性泛函,也就是求
使得
滿足上面 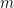 個式子的
個式子的  正是齊次方程
正是齊次方程  的解,基本列運算的目的即在找出所有可消滅子空間
的解,基本列運算的目的即在找出所有可消滅子空間  ,也就是列空間
,也就是列空間  賦予的線性泛函。
賦予的線性泛函。
最後我們以一個例子說明矩陣和線性泛函的子空間表達。考慮
此矩陣的三個列對應以下線性泛函:
對  執行基本列運算得到簡約列梯形式
執行基本列運算得到簡約列梯形式
矩陣 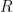 的非零列所對應的線性泛函為
的非零列所對應的線性泛函為
我們知道基本列運算不改變  的列空間和零空間(兩者皆為
的列空間和零空間(兩者皆為  的子空間),所以
的子空間),所以  且
且  。從線性泛函觀點,
。從線性泛函觀點, 擴張出的
擴張出的  的子空間與
的子空間與  擴張出的子空間相同,而且
擴張出的子空間相同,而且  所消滅的
所消滅的  的子空間與
的子空間與  所消滅的子空間也相同,此即
所消滅的子空間也相同,此即  ,或者說線性泛函
,或者說線性泛函  消滅了
消滅了  的列空間
的列空間  。
。
相關閱讀:
留言
張貼留言